Бусидо прыжка или мы пойдем своим путём

Вместо введения

Решил я тут маленькую, но очень гордую задачку… достаточно нетривиальным и необычным способом. Во всяком случае ранее я такого подхода не встречал. Будет немного математики и надеюсь будет интересно. Оговорюсь сразу, во всей статье под скоростью стоит понимать только вертикальную составляющую, так как горизонтальная скорость обрабатывается отдельно. Речь пойдет только про падения и взлёты.

Итак. Вводная задача

1. Персонаж должен прыгать.
2. Персонаж контролируется не физикой юнити, но в виду особенностей используемого контроллера персонажа, мы контролируем только его скорость в каждый момент времени, но не позицию.
3. Прыжок должен регулироваться по двум параметрам: высота прыжка и время прыжка. Так как прыжок штука симметричная (при горизонтальной поверхности время взлета равно времени падения), то для удобства в качестве времени будем брать время взлета, то есть половину всего времени прыжка.

Математика и интегрирование

Формулы расчета начальной скорости и ускорения свободного падения относительно указанных параметров я нашел достаточно быстро (ну не помню я школьную физику настолько хорошо). Вот они, если кому интересно:

\[g = {-2H \over T^2} , V_0 = {2H \over T^2}\] \[g - ускорение, \space H - высота,\space T - время,\space V_0 - начальная \space скорость\]

Запрограммировать такое достаточно просто. На старте рассчитываем числа. Если игрок хочет прыгнуть - устанавливаем скорость в рассчитанную ранее и каждый кадр применяем ускорение к ней, а ее уже применяем к позиции. Попробовали, работает… Но на проверку оказалось… высота установлена 3 метра, а прыгаем мы на 3.2… да и со временем что то не так. Надо разбираться.

Проблемы с формулами я отмел сразу, так как с ними все в порядке. Они бьются со школьным курсом физики, а ставить под сомнения Ньютоновскую механику было бы глупо… да и до релятивистских эффектов как бы далековато, скорости не те. Пришлось снова идти в интернет и вспоминать то, чему меня учили на математическом факультете в течении 6 лет.

По факту, применяя гравитацию и скорость по принципу описанному выше мы получаем аппроксимацию функции прыжка. Как правило оно совпадает с исходной функцией достаточно хорошо на ооооооочень мелких значениях deltaTime. Поэксперементировав, я выяснил что на маленьких значениях FPS прыжок гораздо ниже, чем на высоких. В бой пошли методы решения такого рода проблем: методы численного интегрирования. Применяемый ранее метод в лоб это метод Эйлера, есть симплектический метод Эйлера: в отличии от прямого метода, мы сначала применяем скорость к позиции, а потом наращиваем скорость. Это не решает проблему, но меняет порядок цифр на разных FPS. Был испытан метод Верле и метод Leapfrog (не нашел правильного название на русском, хотя скорее всего оно есть). В первом мы применяем к скорости не ускорение, а среднее ускорение за два последних кадра (текущий и предыдущий). Липфрог предлагает применять к скорости половину ускорения, применять скорость к позиции и потом доприменять оставшуюся половину ускорения, что по сути численно совпадает с методом Верле в конкретно моем случае константного ускорения.

Что же в итоге? Все эти методы дали чуть более лучшиё результат, но не настолько лучший, чтоб я был доволен. Это мой персонаж, и я хочу чтоб он прыгал ровно так, как я хочу. Прошу вроде не много. Тут мне в голову пришла безумная идея, а зачем мне вообще ускорение и его применение? Прыжок это парабола, причем симметричная, со всеми выходящими последствиями. Если знать коэффициенты параболы и текущее положение на этой параболе - мы всегда можем точно высчитать следующее и точно высчитать скорость нужную для этого. Приступим!

Самое интересное (для тех кто не уснул)

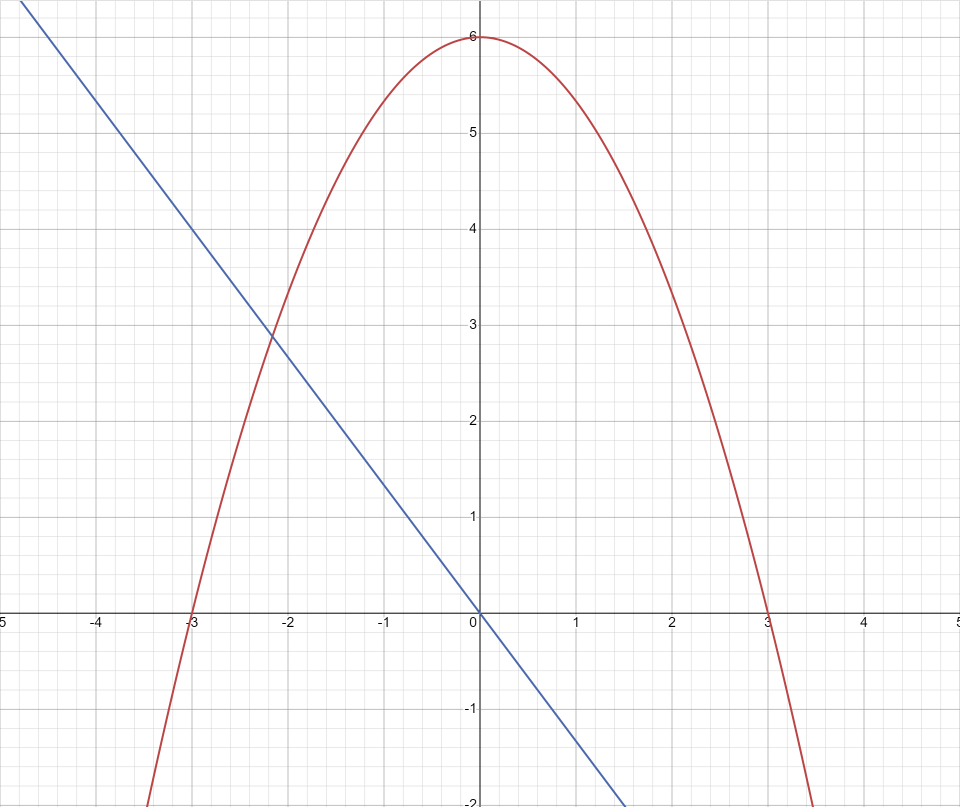
Для начала немного пояснений. Будет использоваться квадратное уравнение зависимости вертикальной позиции от времени. Время не надо понимать как игровое, это некое “локальное” для системы время, которое можно понимать как время от старта прыжка. Для упрощения остальных расчетов, парабола взята таким образом, чтоб вершина ее находилась в нуле. Картинка получается примерно такая:

Если кому интересно то вот такие формулы получаются для обоих графиков:

\[Y = {- H \over T^2}x^2 + H, \space V = {- 2H \over T^2}x\]

Итак, а для чего же нам производная. Ну из курса физики можно вспомнить, что если есть некая функция зависимости позиции от времени, то первая ее производная это функция скорости, вторая это функция ускорения… но она нам не понадобиться. Итогом этих извращений была некая структура:

public struct GravitySolver
{
    public float Height { get; }
    public float ApexTime { get; }
    public float InitialVerticalJumpVelocity { get; }

    private float a;
    private float ad;

    public GravitySolver(float height, float apexTime)
    {
        Height = height;
        ApexTime = apexTime;
        
        a = -Height / (ApexTime * ApexTime);
        ad = 1 / (2 * a);
        
        InitialVerticalJumpVelocity = - 2 * a * ApexTime;
    }

    public float EvalVerticalVelocity(float localTime, ref float deltaTime)
    {
        var nt = localTime + deltaTime;
        if (localTime < 0 && nt > 0) 
        {
            deltaTime = 0 - localTime;
            nt = 0;
        }
        var dx = a * (nt * nt - localTime * localTime);
        
        return dx / deltaTime;
    }

    public float EvalLocalTime(float verticalVelocity) => verticalVelocity * ad;
}

С помощью нее можно вычислить скорость для следующего смещения, а так же подкорректировать изменение “локального” времени. Корректировка состоит в следующем - я всегда хочу чтоб игрок достигал верхней точки, потому тут мы пренебрегаем немного точностью в расчетах времени и изменяем deltaTime таким образом, чтоб при пересечении вершины мы останавливались на ней. Так же данная структура нужна для того, чтоб если в последствии столкновения с чем то в полете скорость поменяется, мы могли скорректировать “локальное” время. Пользуясь тем, что производная скорости в нашем случае линейная функция, по скорости мы всегда можем его вычислить.

Алгоритм применения следующий:

1. Игрок прыгает: делаем скорость равной начальной, устанавливаем “локальное” время в 0 (так как парабола смещена влево, то в -ApexTime).
2. Если по сравнению с предыдущим кадром скорость изменилась и мы по прежнему в воздухе, то вычисляем новое локальное время используя EvalLocalTime, используем далее его.
3. Каждый кадр пока мы находимся в воздухе вызываем EvalVerticalVelocity, применяем полученную скорость, приращиваем “локальное” время.
4. Вы великолепны!

Вместо послесловия

Я не рекомендую данный метод, если нет необходимости в пресижн прыжках. У меня такой необходимости нет, но это была интересная задача для решения. Алгоритм вычислительно получается сложнее, чем просто прибавлять гравитацию каждый шаг, потому применять я вероятно буду его только на главном персонаже. Увы, но для предзаданных кривых он не подходит, потому как нам важны операции с производной и мы во многом тут пользуемся свойствами параболы.